Ethereum 201: HD Wallets

In the previous post in this series, we stepped through Bitcoin Improvement Proposal (BIP) 39: the creation of mnemonic words and 512-bit seeds. This post picks up where we left off — taking the seed and generating actual account private and public keys.

BIP 32 is the standard we’ll examine today, complete with more Python code snippets. BIP 32 is used by Bitcoin, Ethereum, and other blockchains for creating not just one key pair from that seed, but rather virtually unlimited accounts — all of which can be recovered with just one mnemonic sentence or seed.

We’re going to sneak in one more BIP along the way. BIP 44 standardizes a path to describe the intention of a particular account. This will end up influencing how child keys are derived.

To summarize, by the end of this post, you will be familiar three BIPs:

• BIP 39 — “Mnemonic code for generating deterministic keys”
• BIP 32 — “Hierarchical Deterministic Wallets”
• BIP 44 — “Multi-Account Hierarchy for Deterministic Wallets”

Note: if you’d like to skip straight to the code, or want to run it as you read, the implementation is available in a Jupyter Notebook here.

BIP 32 is a specification for creating Hierarchical Deterministic (HD) wallets. What this refers to is that 1) all accounts stem from one root key (hierarchical) and 2) given that root key, all child accounts can be reliably recalculated (deterministic).

The hierarchical nature of HD wallets is easily understood visually. When each “parent” key can produce a number of “child” keys, that produces a tree structure:

A visualization of the hierarchical nature of keys. (Simplified from the original graphic.)

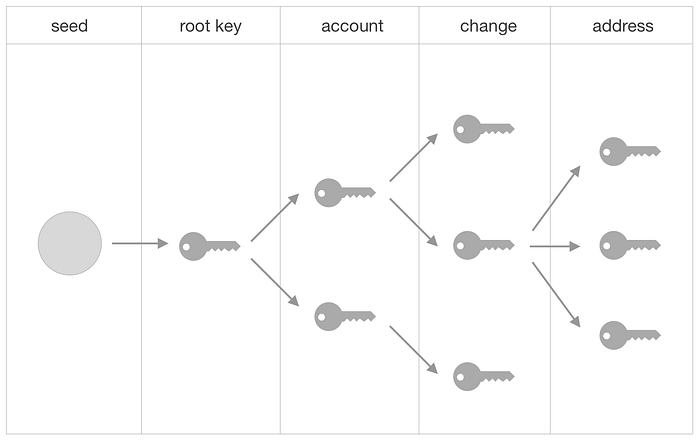
In this post, we’ll start with a seed, derive the root key, then a number of child keys until we reach the desired address.

You’ll notice in the graphic that the tree of accounts has four depths. Each depth has some implied meaning. It turns out those meanings are worth standardizing, too, which lead to the creation of BIP 44. This standard plays an important role in how keys are derived, so we’ll quickly cover it now.

BIP 44 codifies the purpose of each depth level:

m / purpose’ / coin_type’ / account’ / change / address_index

This spec is flexible, but was created specifically for Bitcoin. Each level doesn’t map over to Ethereum perfectly — the change depth, for example, only applies to Bitcoin’s UTXO model — but a “good enough” standard is often better than none. Like BIP 32, BIP 44 has been adopted across a wide range of blockchains, including Ethereum.

You may have seen BIP 44 paths in the wild while using Ethereum hardware or software wallets. When unlocking a wallet in the MyCrypto app, for example, you’ll see the following:

MyCrypto’s unlock address selection — BIP 44 path highlighted in orange.

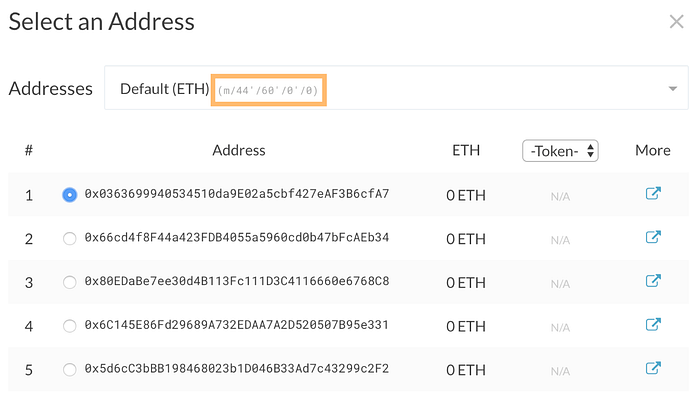
By default, most users of Ethereum are utilizing an address with a derivation path of m/44'/60'/0'/0/0. Briefly explained:

• The apostrophes (e.g., in the first three levels) indicate that the value is hardened. This is a security feature we’ll learn the implications of soon.
• m — is a convention; nothing to read into here.
• 44 — purpose — this path follows the BIP 44 standard.
• 60 — coin_type — 60 indicates the Ethereum network. The list of “registered coin types” can be found here.
• 0 — account — intended to represent different types of wallet users. For example, a business may have one branch of accounts for an accounting department and another for a sales team. It’s a zero-based index.
• 0 — change — mostly Bitcoin’s cup of tea. Typically remains 0 for Ethereum addresses.
• 0 — address_index — finally, the index of the account you’re using. This is also a zero-based index, so index 0 is the first available account. If you have ten accounts, the last’s derivation path is m/44'/60'/0'/0/9.

That’s the whole gist of BIP 44. We’re almost done with the context and ready for some code — stay with me!

BIP 32 requires we start with a seed, typically one produced by a BIP 39 implementation. From that seed will spring as many accounts as you could ever conceivably need. For this example, we’ll start with one of the seeds provided in the standard’s test vectors:

seed = 'fffcf9f6f3f0edeae7e4e1dedbd8d5d2cfccc9c6c3c0bdbab7b4b1aeaba8a5a29f9c999693908d8a8784817e7b7875726f6c696663605d5a5754514e4b484542'

The first goal is to convert the seed into what is called a master key or root key. “Root” is illustrative, in that all derivative keys will branch off from it.

For a preview of where we’re headed, you can plug the seed above into an address generator like this one and see the resulting root key and derived addresses. Make sure to paste the seed above, without quotes, into the BIP 39 Seed field and select “ETH — Ethereum” from the Coin options.

Partial screenshot from Ian Coleman’s account generator website

There’s a lot going on under the hood to produce those values, so let’s take it one step at a time.

Note: the upcoming formulas regularly rely on hash functions and elliptic curve cryptography. The intricacies of those concepts are out of the scope of this article. Instead, you’ll find an end-to-end implementation with an explanation of the big picture.

The root key is generated in a couple steps:

• I = HMAC-SHA512(Key = “Bitcoin seed”, Data = seed)
• Split I into two 32-byte sequences, L and R.
• Use parse256(L) as master secret key, and R as master chain code.

In Python:

import binascii
import hmac
import hashlib
# the HMAC-SHA512 `key` and `data` must be bytes:
seed_bytes = binascii.unhexlify(seed)
I = hmac.new(b'Bitcoin seed', seed_bytes, hashlib.sha512).digest()
L, R = I[:32], I[32:]
master_private_key = int.from_bytes(L, 'big')
master_chain_code = R

A good first step! The master private key and chain code will be used to derive all subsequent child keys. The chain code serves as entropy.

We haven’t exactly gotten the root key yet, though. The root key is typically represented as an extended private key (xprv). Defined in the BIP 32 spec, extended private keys are a Base58 encoding of the private key, chain code, and some additional metadata. We’ll derive that next.

Fun fact: Base58 encoding was created specifically for Bitcoin. It’s just like Base64, but without some commonly misinterpreted characters , for example: 0, O, I, and l. So, binary values can be converted to the following letters and numbers: 123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz.

As seen in the last account generator screenshot, we’re going to end up with the following extended private key:

xprv9s21ZrQH143K31xYSDQpPDxsXRTUcvj2iNHm5NUtrGiGG5e2DtALGdso3pGz6ssrdK4PFmM8NSpSBHNqPqm55Qn3LqFtT2emdEXVYsCzC2U

You’ll notice 1) there are no zeros, uppercase o’s, uppercase i’s, or lowercase l’s, and 2) the first four characters are xprv. xprv is a deliberate sequence of four bytes to let us know we’re looking at an extended private key intended for use on mainnet.

Per the spec, 78 bytes are encoded to derive extended keys:

• 4 bytes: version bytes (mainnet: 0x0488B21E public, 0x0488ADE4 private; testnet: 0x043587CF public, 0x04358394 private)
• 1 byte: depth (0x00 for master nodes, 0x01 for level-1 derived keys, etc.)
• 4 bytes: the fingerprint of the parent key
• 4 bytes: the child number
• 32 bytes: the chain code
• 33 bytes: the public or private key data

In Python, this might look like:

import base58
VERSION_BYTES = {
    'mainnet_public': binascii.unhexlify('0488b21e'),
    'mainnet_private': binascii.unhexlify('0488ade4'),
    'testnet_public': binascii.unhexlify('043587cf'),
    'testnet_private': binascii.unhexlify('04358394'),
}
version_bytes = VERSION_BYTES['mainnet_private']
depth_byte = b'\x00'
parent_fingerprint = b'\x00' * 4
child_number_bytes = b'\x00' * 4
key_bytes = b'\x00' + L
all_parts = (
    version_bytes,      # 4 bytes  
    depth_byte,         # 1 byte
    parent_fingerprint,  # 4 bytes
    child_number_bytes, # 4 bytes
    master_chain_code,  # 32 bytes
    key_bytes,          # 33 bytes
)
all_bytes = b''.join(all_parts)
root_key = base58.b58encode_check(all_bytes).decode('utf8')
print(root_key)
# xprv9s21ZrQH143K...T2emdEXVYsCzC2U

Root key: ✅

In the case of the root key, most of the additional metadata is zeroed out:

• We know the root key is the first node in the tree (i.e., a depth of zero), so depth_byte is intuitive enough — one empty byte.
• We’ll explore fingerprints and child numbers shortly, when we need to calculate them for child accounts, but for the first around they are each represented as four empty bytes.
• The spec requires 33 bytes for key data. The master private key, L, is only 32, so the front is padded with one empty byte.

Great, we’ve got a root key. How about accounts we can actually use — with private keys and public addresses?

At a high level, we’ll need to derive the child keys for each depth in the path we desire. So, if we want to generate the keys for the address at path m/44'/60'/0'/0/0, we’re going to end up running a child key derivation function five times — once per numerical value in the path.

In Python, we’ll represent the path as a tuple, so we have something to iterate over. Pulling straight from the spec:

Each extended key has 2³¹ normal child keys, and 2³¹ hardened child keys. Each of these child keys has an index. The normal child keys use indices 0 through 2³¹–1. The hardened child keys use indices 2³¹ through 2³²–1.

So, if the value is hardened, then we simply add 2³¹ to that number. For example:

# Break each depth into integers (m/44'/60'/0'/0/0)
#    e.g. (44, 60, 0, 0, 0)
# If hardened, add 2**31 to the number:
#    e.g. (44 + 2**31, 60 + 2**31, 0 + 2**31, 0, 0)
path_numbers = (2147483692, 2147483708, 2147483648, 0, 0)

What does a hardened path imply? It’s a security feature; private keys are used in the generation of hardened keys, while non-hardened (or normal) keys are generated using public keys. This has implications on what keys are capable of.

Normal extended public keys (xpub) may be used to create child public keys, for example. A commonly cited use case is providing a storefront with an extended public key, which can be used to derive a new child public address to receive funds for each sale. No private keys ever live on the server, so there’s no risk of them leaking if the server is compromised.

If you fancy a deeper dive, these two StackExchange answers might be a good place to start.

Back to business. In order to derive an extended child private key, we’ll need the same variables used to derive the root key: private key, chain code, fingerprint, depth, and child number. At the moment, we’ve only derived the root key and its constituent parts, leaving us with:

depth = 0
parent_fingerprint = None
child_number = None
private_key = master_private_key
chain_code = master_chain_code

We’ve discussed depth, private keys and chain codes. The child number is simply the current path integer from the path_numbers tuple. The first time through the child key derivation function, child_number will be equal to 2147483692. On the fifth and final iteration, child_number will be 0.

Fingerprints are a little more involved. Per the BIP 32 standard:

Extended keys can be identified by the Hash160 (RIPEMD160 after SHA256) of the serialized ECDSA public key K, ignoring the chain code. […] The first 32 bits of the identifier are called the key fingerprint. […] Note that the fingerprint of the parent only serves as a fast way to detect parent and child nodes in software…

That’s a mouthful. Summarized, a fingerprint is a link from a child key to its parent, and the BIP 32 standard specifies a formula to derive those four bytes.

The formula is a mix of hash functions and elliptic curve cryptography, so we’re just gonna tuck that magic away here:

from ecdsa import SECP256k1
from ecdsa.ecdsa import Public_key
SECP256k1_GEN = SECP256k1.generator
def serialize_curve_point(p):
   x, y = K.x(), K.y()
   if y & 1:
      return b'\x03' + x.to_bytes(32, 'big')
   else:
      return b'\x02' + x.to_bytes(32, 'big')
def curve_point_from_int(k):
   return Public_key(SECP256k1_GEN, SECP256k1_GEN * k).point
def fingerprint_from_private_key(k):
   K = curve_point_from_int(k)
   K_compressed = serialize_curve_point(K)
   identifier = hashlib.new(
      'ripemd160',
      hashlib.sha256(K_compressed).digest(),
   ).digest()
   return identifier[:4]

Finally, let’s address that child key derivation function that we expect to run five times. The function takes the private key, chain code and child number as inputs and returns the child private key and child chain code.

The first thing the function does is check to see whether it’ll be deriving a hardened or normal key. Remember from earlier discussion that private keys are used to derive hardened keys, while public keys (e.g., curve_point_from_int(private_key)) derive normal keys.

The rest of the function should look similar to the derivation of the master private key and master chain code:

# Review of master private key and chain code derivation:
I = hmac.new(b'Bitcoin seed', seed_bytes, hashlib.sha512).digest()
L, R = I[:32], I[32:]
master_private_key = int.from_bytes(L, 'big')
master_chain_code = R

This time, the parent chain code is used in lieu of b'Bitcoin seed' and the data is the child number appended to the (hardened or normal) key data:

SECP256k1_ORD = SECP256k1.order
def derive_ext_private_key(private_key, chain_code, child_number):
    if child_number >= 2 ** 31:
        # Generate a hardened key
        data = b'\x00' + private_key.to_bytes(32, 'big')
    else:
        # Generate a non-hardened key
        p = curve_point_from_int(private_key)
        data = serialize_curve_point(p)
    data += child_number.to_bytes(4, 'big')
    hmac_bytes = hmac.new(chain_code, data, hashlib.sha512).digest()
    L, R = hmac_bytes[:32], hmac_bytes[32:]
    L_as_int = int.from_bytes(L, 'big')
    child_private_key = (L_as_int + private_key) % SECP256k1_ORD
    child_chain_code = R
    return (child_private_key, child_chain_code)

There’s a lot packed in there. If you’re still with me, let’s take it home. Now that we have all the pieces in place, it’s time to iterate over the path numbers and recursively update each value:

path_numbers = (2147483692, 2147483708, 2147483648, 0, 0)
depth = 0
parent_fingerprint = None
child_number = None
private_key = master_private_key
chain_code = master_chain_code
for i in path_numbers:
   depth += 1
   child_number = i
   parent_fingerprint = fingerprint_from_private_key(private_key)
   private_key, chain_code = derive_ext_child_key(private_key)

Once finished, you’ve got the private key for the account at path m/44'/60'/0'/0/0! The hard part is done. You can compare your result to the one in Ian Coleman’s generator by displaying the hex value of the private key:

print(f'private key: {hex(private_key)}')
# private key: 0x3c4cf049f83a5870ab31c396a0d46783c3e3974da1364ea5a2477548d36b5f8f

Private key: ✅

The public key can be derived from the private key with more elliptic curve cryptography:

p = curve_point_from_int(private_key)
public_key_bytes = serialize_curve_point(p)
print(f'public key: 0x{public_key_bytes.hex()}')
# public key: 0x024c8f4044470bd42b81a8b233e2f954b63f4ee2c32c8d44288b44188754e2042e

Public key: ✅

If we ever want to receive any funds, we’re gonna need a public address, too. Addresses are derived from the public key. Specifically, a public address is the last 20 bytes of the Keccak-256 hash of the public key points. In Python:

from eth_utils import keccak
digest = keccak(x.to_bytes(32, 'big') + y.to_bytes(32, 'big'))
address = '0x' + digest[-20:].hex()
print(f'public address: {address}')
# public address: 0xbbec2620cb01adae3f96e1fa39f997f06bfb7ca0

Public address: ✅

Lets put a bow on the post by deriving the extended private key (xprv) for the account at this path. Deriving this value is the best way to know you’ve done the whole process correctly. The BIP 32 standard includes some test vectors for HD wallet developers to verify that, given a seed and a desired path, their software can derive the correct xprv and xpub values.

We’ll use the same formula we used to derive the root key, but this time the metadata contains more than empty bytes:

version_bytes = VERSION_BYTES['mainnet_private']
depth_byte = depth.to_bytes(1, 'big')
child_number_bytes = child_number.to_bytes(4, 'big')
key_bytes = b'\x00' + private_key.to_bytes(32, 'big')
all_parts = (
    version_bytes,      # 4 bytes  
    depth_byte,         # 1 byte
    parent_fingerprint,  # 4 bytes
    child_number_bytes, # 4 bytes
    chain_code,         # 32 bytes
    key_bytes,          # 33 bytes
)
all_bytes = b''.join(all_parts)
extended_private_key = base58.b58encode_check(all_bytes).decode('utf8')

If you’re coding along at home, you should end up with the following xprv:

print(f'extended private key: {extended_private_key}')
# extended private key: xprvA2vDkmMuK1Ae2eF92xyQpn6qZzHoGTnV5hXrBw7UExUTXeMFTZDLF7cRD6vhR785RMF2EC6mAo3ojRqFEUU8VxTSzGq1jvmXSBTxoCGSSVG

Extended private key: ✅

That’s all folks! Thanks for playing along at home. There’s plenty more to explore — we didn’t derive any extended public keys (xpub) or dig too deep into hardened keys, but you should now have the context required to explore whichever rabbit holes call your name.

Again, if you’re interested in the Jupyter notebook with this code, you can find that here. If you’d like to explore a comprehensive Python implementation, py-hdwallet is a newer project maintained by Ethereum Foundation. The code in this post is a simplified version of what can be found in py-hdwallet.

Disclaimer: the code in this post is for educational purposes only. Make responsible choices (e.g., use mature, audited tools) when deciding where to store your assets.